Utilities Library¶

These pages refer to various utility functions used across theframework. These functions and types are the subject of a dedicated library and altogether, besides of the third-party dependencies, represent a lowest level of the framework’s API.

group numerical-utils

Typedefs

typedef struct na64dp_KleinScorer na64dp_KleinScorer_t¶

A generalized Kahan-Babuška summation algorithm state instance.

Declares reentrant state object for the Klein’s summation algorithm present in doi:https://doi.org/10.1007%2Fs00607-005-0139-x . An \(i\)-th algorithm have the error \( O(n(log_2 (n) \epsilon)^{i+1}) \).

Usage implies initialization, multiple iterative increment operations and result retreival with corresponding functions.

typedef struct na64dp_Covariance na64dp_Covariance_t¶

A running covariance coefficient calculus for two variables.

Explots the running approach to calculate co-moment of the relative distribution.

For summation, the Klein’s scorer is applied as a reentrant state.

typedef struct na64dp_CovarianceMatrix na64dp_CovarianceMatrix_t¶

Unweighted covariance matrix implementation.

Number of independent components obeys triangular number series.

Functions

int na64sw_projected_lines_intersection(const na64sw_Float_t *k1, const na64sw_Float_t *k2, const na64sw_Float_t *k3, const na64sw_Float_t *r01, const na64sw_Float_t *r02, na64sw_Float_t *x1, na64sw_Float_t *x2)¶

Finds “intersection” points defined by two non-complanar measurements.

A solution for rather common case of what is assumed to be a “track point”, when it should be defined by 1D measurements of two planes. Each “measurement” define a line in space, but two given lines do not intersect (despite are may be very close) — skew lines case.

The proposed solution is, having some “sight” direction, obtain a “seen” intersection. For most of the cases this direction is defined either by closest approach (perpendicular to both lines), or by expected ionizing particle direction.

Found solution \(\vec{x1}, \vec{x2}\) is a line segment directed according to “sight” direction with endpoints lying on first and second line. Applications may use those points independently or take an average to define a spatial point of approximate hit position.

[in] k1 direction vector of 1st measurement
[in] k2 direction vector of 2nd measurement
[in] k3 “sight” direction; if NULL — calculated as closest approach
[in] r01 some point on 1st line
[in] r02 some point on 2nd line
[out] x1 “intersection” point on first line (or equidistant point if x2 is NULL)
[out] x2 “intersection” point on first line (or NULL)

Note

Uses GSL inside (thus, may invoke GSL error handler in some circumustances).

Returns: 0 on success, -1 if no solution exists

Double_t langaus(Double_t x, Double_t width, Double_t mp, Double_t area, Double_t sigma, Int_t np = 100, Double_t sc = 5.0)¶

A convoluted Landau and Gauss distribution functions with scaling parameter.

This function is taken from official ROOT tutorial. See, e.g.: https://root.cern/doc/v608/langaus_8C.html

Fit parameters:

In the Landau distribution (represented by the CERNLIB approximation), the maximum is located at x=-0.22278298 (defined in

gLandauFMax global const) with the location parameter=0. This shift is corrected within this function, so that the actual maximum is identical to the MP parameter.

Parameters

x – variable
width – (scale) parameter of Landau density
mp – most Probable (MP, location) parameter of Landau density
area – total area (integral -inf to inf, normalization constant)
sigma – width (sigma) of convoluted Gaussian function
np – number of convolution steps
sc – convolution extends to +-sc Gaussian sigmas

Double_t langausfun(Double_t *x, Double_t *par)¶: langaus() alias for ROOT’s fitting routines

std::pair<TF1*, bool> langausfit(TH1F *his, Double_t *fitrange, Double_t *startvalues, Double_t *parlimitslo, Double_t *parlimitshi, const char *fitOpts, Double_t *fitparams, Double_t *fiterrors, Double_t &chiSqr, Int_t &ndf)¶

Will fit provided histogram with langaus() function with standard ROOT fitting algorithms returning function and model parameters.

Note

This function allocates TF1 instance on heap. One has to delete it afterwards.

Parameters

his – [in] histogram to fit
fitrange – [in] lo and hi boundaries of fit range
startvalues – [in] 4-element, reasonable start values for the fit
parlimitslo – [in] 4-element, lower parameter limits
parlimitshi – [in] 4-element, upper parameter limits
fitOpts – [in] sets fitting options. Default is “LRQ0” (when NULL)
fitparams – [out] 4-element returns the final fit parameters
fiterrors – [out] 4-element returns the final fit errors
chiSqr – [out] returns the chi square
ndf – [out] returns ndf

Returns

an instance of TF1 representing fit function

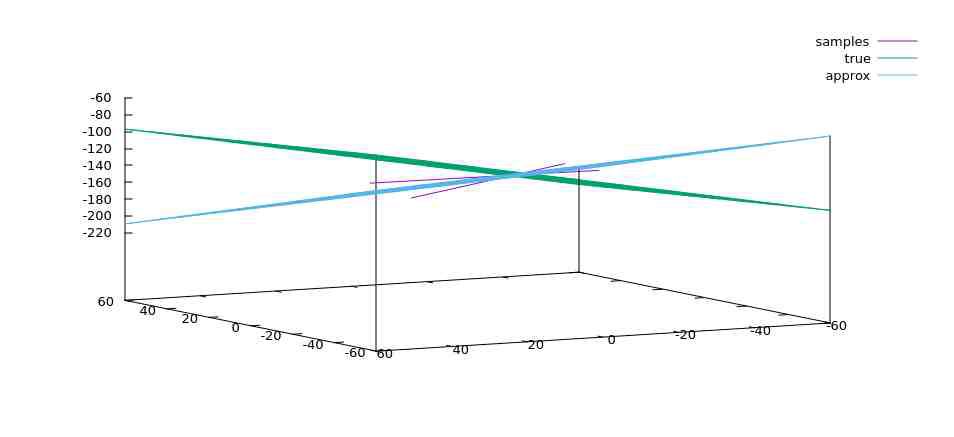
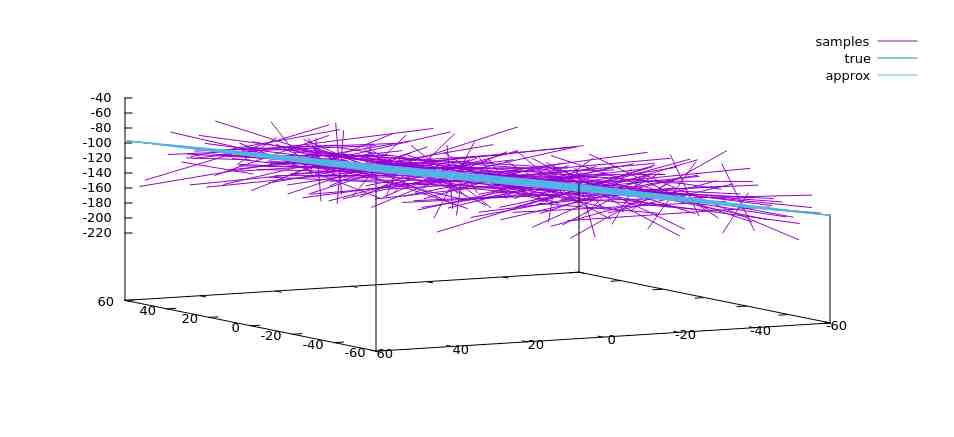
int na64sw_fit_line_segments_w_plane_unweighted(na64sw_Float_t *segments[], size_t nSegments, size_t nDims, na64sw_Float_t *A, na64sw_Float_t *N)¶

Fits the given set of linear segments with plane.

Original method is taken from documentation of Geometric Tools geomToolsSegmentsOrPlane .

_images/plane-fit-approx_few.jpg

_images/plane-fit-approx_multiple.jpg

void na64dp_sum_klein_init(na64dp_KleinScorer_t *S)¶: (Re-)initializes Klein scorer

void na64dp_sum_klein_add(na64dp_KleinScorer_t *S, double v)¶: Adds a value to Klein scorer

double na64dp_sum_klein_result(const na64dp_KleinScorer_t *S)¶: Returns sum of Klein scorer.

void na64dp_cov_init(na64dp_Covariance_t *ptr)¶: (Re-)initializes running Pearson’s covariance calculus

void na64dp_cov_account(na64dp_Covariance_t *ptr, double x, double y)¶: Adds variable pair to consideration.

double na64dp_covariance_get(const na64dp_Covariance_t *ptr)¶: Get the (population) covariance result from current state.

void na64dp_mcov_init(na64dp_CovarianceMatrix_t *ptr, unsigned short d)¶: Initializes covariance matrix for vector of d components.

void na64dp_mcov_account(na64dp_CovarianceMatrix_t *ptr, const double *v)¶: Adds vector to consideration.

double na64dp_mcov(na64dp_CovarianceMatrix_t *ptr, int i, int j)¶: Returns covariance of i-th and j-th variables.

void na64dp_mcov_free(na64dp_CovarianceMatrix_t *ptr)¶: Frees covariance matrix.

template<Arity_t NT, typename SeqT> class CartesianProduct¶

#include <cartesian-product.hh>

Helper class representing stateful generator for cartesian product.

Initialized with a sequence of homogeneous STL containers, implements an iterator over cartesian product results (pairs, triplets, quadruplets, etc).

Public Functions

inline bool operator>>(std::array<typename SeqT::value_type, NT> &dest)¶: Writes set of IDs to given destination, if possible. If not, returns false

template<typename T, Arity_t NT> struct CartesianProductCollections : protected std::array<std::vector<T>, NT>¶

#include <cartesian-product.hh>

Product result in array of fixed arity.

Public Functions

inline void add(Arity_t n, const T &element)¶: Adds new element into n-th set.

inline void clear()¶: Clears collected sets.

union Vec3T¶

#include <linalg.hh>

3-dim spatial vector representation used in the lib

Public Functions

inline FloatT operator[](int i) const¶: Component getter.

inline FloatT &operator[](int i)¶: Component reference getter.

template<typename FloatT2> inline FloatT operator*(const Vec3T<FloatT2> &b) const¶: Scalar product.

template<typename FloatT2> inline Vec3T<FloatT> operator*(FloatT2 a) const¶: Vector multiplied by number.

template<typename FloatT2> inline Vec3T<FloatT> &operator*=(FloatT2 a)¶: In-place multiplication by number.

template<typename FloatT2> inline Vec3T<FloatT> operator/(FloatT2 a) const¶: Vector divided by number.

template<typename FloatT2> inline Vec3T<FloatT> &operator/=(FloatT2 a)¶: In-place division by number.

template<typename FloatT2> inline Vec3T<FloatT> operator+(const Vec3T<FloatT2> &b) const¶: Vector sum.

template<typename FloatT2> inline Vec3T<FloatT> &operator+=(const Vec3T<FloatT2> &b)¶: In-place vector sum.

template<typename FloatT2> inline Vec3T<FloatT> operator-(const Vec3T<FloatT2> &b) const¶: Vector sub.

template<typename FloatT2> inline Vec3T<FloatT> &operator-=(const Vec3T<FloatT2> &b)¶: In-place vector sub.

template<typename FloatT2> inline Vec3T<FloatT> cross(const Vec3T<FloatT2> &b) const¶: Vector cross product.

inline FloatT norm() const¶: Returns norm of the vector.

inline Vec3T<FloatT> unit() const¶: Returns unit (orth) of this vector.

inline Vec3T<FloatT> operator-() const¶: Unary minus (inversion) operator.

Public Members

FloatT r[3]¶: Data acessed by index.

struct na64dp::util::Vec3T::[anonymous] c¶: Data acessed by component name.

union Matrix3T¶

#include <linalg.hh>

3x3 matrix representation

Public Functions

inline const FloatT *operator[](int n) const¶: Returns RO-ptr to the 1st element in Nth row.

inline FloatT *operator[](int n)¶: Returns RW-ptr to the 1st element in Nth row.

template<typename FloatT2> inline Vec3T<FloatT> operator*(const Vec3T<FloatT2> &v) const¶: Matrix.Vector product.

template<typename FloatT2> inline Matrix3T<FloatT> operator*(const Matrix3T<FloatT2> &bm) const¶: Matrix.Matrix product.

inline FloatT det() const¶

Matrix determinant

Directly computes matrix determinant based on first line.

Warning

Must not be used for general purpose as can be numerically unstable for small values in first line.

Matrix3T<FloatT> inv() const¶: Returns inverted matrix.

Warning

Uses direct calculus for inversion, not recommended for general use as it is numerically unstable.

Matrix3T<FloatT> transposed() const¶: Returns transposed matrix.

Public Members

FloatT cm[3][3]¶: Data representations.

FloatT m[9]¶

struct na64dp_KleinScorer¶

#include <sums.h>

A generalized Kahan-Babuška summation algorithm state instance.

Declares reentrant state object for the Klein’s summation algorithm present in doi:https://doi.org/10.1007%2Fs00607-005-0139-x . An \(i\)-th algorithm have the error \( O(n(log_2 (n) \epsilon)^{i+1}) \).

Usage implies initialization, multiple iterative increment operations and result retreival with corresponding functions.

Subclassed by na64dp::numerical::KleinScorer

struct na64dp_Covariance¶

#include <sums.h>

A running covariance coefficient calculus for two variables.

Explots the running approach to calculate co-moment of the relative distribution.

For summation, the Klein’s scorer is applied as a reentrant state.

Subclassed by na64dp::numerical::CorrelationScorer

Public Members

unsigned long n¶: Number of pairs being considered

na64dp_KleinScorer_t xMean¶: < Current mean of X samples

na64dp_KleinScorer_t yMean¶: < Current mean of Y samples

na64dp_KleinScorer_t d2x¶: < Sum of X deviation squares

na64dp_KleinScorer_t d2y¶: < Sum of Y deviation squares

na64dp_KleinScorer_t rS¶: Sum of relative deviation products

struct na64dp_CovarianceMatrix¶

#include <sums.h>

Unweighted covariance matrix implementation.

Number of independent components obeys triangular number series.

Subclassed by na64dp::numerical::CovarianceMatrix

Public Members

unsigned short d¶: Number of components in vector

unsigned long n¶: Number of considered samples

na64dp_KleinScorer_t *means¶: Array of mean scorers

na64dp_KleinScorer_t *sqds¶: Array of squared deviation scorers

na64dp_KleinScorer_t *covs¶: Sum of relative deviation products (co-moments)

struct Transformation¶

#include <transformations.hh>

Combined transformation (rotation, translation, scaling and shear)

This class defines complete set of affine transformation between two \(\mathbb{R}_3\) spaces in terms of:

a translation vector \(\vec{o}\)
a rotation matrix \(R\)
a scale/shear matrix \(W\) composed from local bases vectors \(\vec{u}\), \(\vec{v}\), \(\vec{w}\).

As a result, having a measurement vector \(\vec{m}\) expressed in local (detector’s) frame one can obtain global coordinates as:

\[ \vec{r} = T(\vec{m}) = \vec{o} + R (W \vec{m}) \]

This class can be constructed from (and can provide back) quantities that are more convenient to deal with:

rotation angles triplet in certain (user-defined) order
offset vector
local bases vectors of dimensions length (usually corresponding to detector’s sensitive volume).

Todo:

Support or combination (merging) operations and transformations chaining

Full support for inversion

Method for covariance transformation

Note

Matrix of affine transform (rotation and scaling in local basis) can be used to “rotate” the covariance.

Warning

Dealing with angles, please note that due to mathematical ambiguity returned angular values of \(> \pi/2\) can not always be spatially resolved matching the exact input.

Public Functions

Transformation()¶: Creates identity transformation.

Transformation(const Vec3 &offset_, const Vec3 &u_, const Vec3 &v_, const Vec3 &w_, Float_t alpha, Float_t beta, Float_t gamma, na64sw_RotationOrder rotationOrder = gStdRotationOrder, bool invertOffset = false)¶: Creates transformation defined by values.

Transformation(const Transformation&)¶: Copy ctr.

inline bool is_inverse() const¶: Returns true for reverse transformation.

inline const Vec3 &o() const¶

Returns offset in global (lab) frame.

Offset vector set for the transformation.

Note

Returns same value of same meaning for direct and inverted transform.

inline void o(const Vec3 &o_)¶

Sets the offset vector (in lab frame)

Does not invalidate the cache with affine transformations

inline const Vec3 &u() const¶: Returns 1st basis vector.

inline Vec3 gU() const¶: Returns 1st basis vector rotated to the global frame.

inline void u(const Vec3 &u_)¶

Sets 1st basis vector.

Invalidates the cache of affine transformations

inline const Vec3 &v() const¶: Returns 2nd basis vector.

inline Vec3 gV() const¶: Returns 2nd basis vector rotated to the global frame.

inline void v(const Vec3 &v_)¶

Sets 2nd basis vector.

Invalidates the cache of affine transformations

inline const Vec3 &w() const¶: Returns 3rd basis vector.

inline Vec3 gW() const¶: Returns 3rd basis vector rotated to the global frame.

inline void w(const Vec3 &w_)¶

Sets 3rd basis vector.

Invalidates the cache of affine transformations

inline na64sw_RotationOrder rotation_order() const¶: Returns rotation order.

inline void rotation_order(na64sw_RotationOrder order_)¶

Sets rotation order.

Invalidates cache of affine transformations

Float_t angle(int n) const¶

retruns N-th rotation angle

Returns one of three rotation angles (called in ctr as alpha, beta, gamma) that can have different meaning depending on rotation order set.

Throws: Runtime – error if index is out of range.

void angle(int n, Float_t)¶

Sets N-th rotation angle.

Sets one of three rotation angles (called in ctr as alpha, beta, gamma) that can have different meaning depending on rotation order set. Invalidates cache of affine transformations.

Throws: Runtime – error if index is out of range.

const Matrix3 &rotation_matrix() const¶: Returns rotation matrix.

const Matrix3 &basis() const¶: Returns shear-and-scale transformation matrix built on local basis.

const Matrix3 &affine_matrix() const¶: Returns full affine transform matrix (without global offset)

inline void apply(Vec3 &m) const¶: Applies spatial transformation to the vector, modifying it.

inline Vec3 operator()(const Vec3 &m) const¶: Shortcut for copying form of apply()

Transformation inverted() const¶: Returns inverse affine transformation.

na64dp::util::Vec3T.c: Data acessed by component name.

group numerical-utils-online-stats

class KleinScorer : protected na64dp_KleinScorer ¶

#include <online.hh>

C++ interface over C implementation of Klein’s scorer.